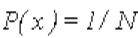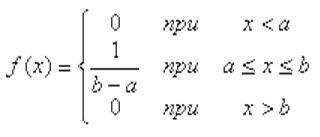Случайной называется величина, которая при испытаниях принимает одно из возможных значений, наперед неизвестно какое.
Случайные величины бывают дискретные или непрерывные. Дискретная величина - например, число выстрелов. Непрерывная величина – значения заполняют некий промежуток – например, дистанция выстрела снаряда от 5 до 5,3 км.
Вероятность - оценка возможности появления случайного события.
Законом распределения случайной величины
называется соответствие между значением величины, которое она приняла в результате испытаний, и вероятностью появления этого значения.
Биномиальное распределение случайной величины

p – вероятность наступления события в одном испытании.
q – вероятность не наступления события в одном испытании q = (1-p)
n – количество испытаний
k – предполагаемое количество наступления желаемого события
Формула Бернулли, позволяет вычислить вероятность того, что событие появится в n испытаниях ровно k раз.
Пуассоновское распределение.
Ситуация, когда вероятность появления события в каждом испытании близка к 0 (такие события называются редкими явлениями), а количество испытаний велико. Вероятность того, что в n независимых испытаниях событие наступит m раз, приближенно равна:
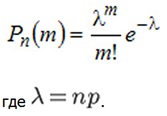
n – количество испытаний
m – предполагаемое наступление желаемого события
p- вероятность наступления события в одном испытании
Пример: Установлено, что при транспортировке в вагоне более 5000 изделий портится в среднем одно изделие. Найти вероятность того, что испортится три изделия. (0,06).
Нормальное (гаусовское) распределение
Это основной закон теории вероятностей. В пределе все законы стремятся к нормальным законам распределения. Сумма бесконечного числа случайных величин, распределенных по любым законам, в итоге приобретает нормальный закон распределения.
Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения равна:
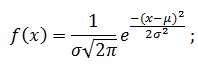
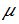 – Математическим ожиданием дискретной случайной величины называют сумму произведений возможных значений случайной величины на вероятности их появления
– Математическим ожиданием дискретной случайной величины называют сумму произведений возможных значений случайной величины на вероятности их появления
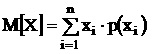
Дисперсия - для оценки степени разброса (отклонения) какого-то показателя от его среднего значения используются понятия дисперсии.
Дисперсия выборки или выборочная дисперсия – это мера изменчивости переменной. Дисперсия вычисляется по формуле:
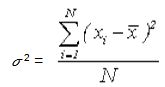
где х — выборочное среднее,
N — число наблюдений в выборке.
Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны.
 - среднеквадратическое отклонение случайной величины (квадратный корень из дисперсии.)
- среднеквадратическое отклонение случайной величины (квадратный корень из дисперсии.)
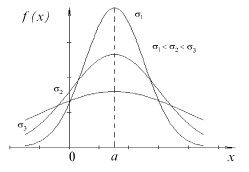 График функции нормального распределения, как видно из рисунка, имеет вид куполо¬образной кривой, называемой
График функции нормального распределения, как видно из рисунка, имеет вид куполо¬образной кривой, называемой
Гауссовой, точка максимума имеет координаты 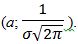 Значит, эта ордината убывает с возрастанием значения
Значит, эта ордината убывает с возрастанием значения  (кривая «сжимается» к оси Ох) и возрастает с убыванием значения
(кривая «сжимается» к оси Ох) и возрастает с убыванием значения  (кривая «растягивается» в положительном направлении оси Оу). Изменение значений параметра u (при неизменном значении
(кривая «растягивается» в положительном направлении оси Оу). Изменение значений параметра u (при неизменном значении  ) не влияет на форму кривой, а лишь перемещает кривую вдоль оси Ох.
Нормальное распределение с параметрами
) не влияет на форму кривой, а лишь перемещает кривую вдоль оси Ох.
Нормальное распределение с параметрами 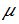 =0 и
=0 и  =1 называется нормированным. Функция распределения случайной величины в этом случае будет иметь вид:
=1 называется нормированным. Функция распределения случайной величины в этом случае будет иметь вид:
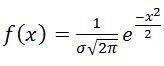
Для 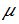 =0,
=0,  =1 график принимает вид:
=1 график принимает вид:
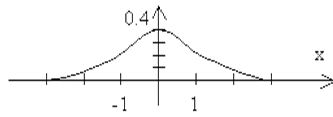
Эта кривая при 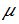 =0,
=0,  =1 получила статус стандарта, ее называют единичной нормальной кривой, то есть любые собранные данные стремятся преобразовать так, чтобы кривая их распределения была максимально близка к этой стандартной кривой.
=1 получила статус стандарта, ее называют единичной нормальной кривой, то есть любые собранные данные стремятся преобразовать так, чтобы кривая их распределения была максимально близка к этой стандартной кривой.
Нормализованную кривую изобрели для решения задач теории вероятности, но оказалось на практике, что она отлично аппроксимирует распределение частот при большом числе наблюдений для множества переменных
Показательное (экспоненциальное) распределение
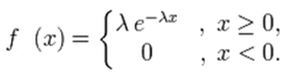
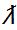 - интенсивность (среднее число событий в единицу времени)
- интенсивность (среднее число событий в единицу времени)
Непрерывная случайная величина X, функция плотности которой задается данным выражением, называется случайной величиной, имеющей показательное, или экспоненциальное, распределение.
Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению.
Как видно из формулы , показательное распределение определяется только одним параметром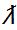 . Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров.
. Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров.
График функций показательного распределения имеют вид:
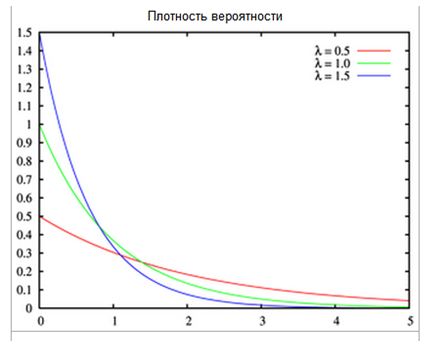
Вероятность попадания случайной величины X в интервал [a - b]:
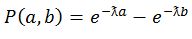
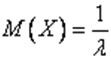 ,математическое ожидание
,математическое ожидание
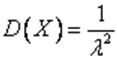 , дисперсия
, дисперсия
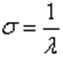 ,среднеквадратическое отклонение
,среднеквадратическое отклонение
Таким образом, для показательного распределения характерно, что среднее квадратическое отклонение численно равно математическому ожиданию.
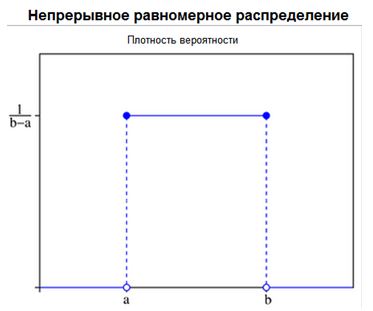
Равномерное распределение
Равномерное распределение вероятностей является простейшим и может быть как дискретным, так и непрерывным. Дискретное равномерное распределение – это такое распределение, для которого вероятность каждого из значений СВ одна и та же, то есть:
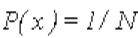
где N – количество возможных значений СВ.
Распределение вероятностей непрерывной CВ Х, принимающие все свои значения из отрезка [а;b] называется равномерным, если ее плотность вероятности на этом отрезке постоянна, а вне его равна нулю:
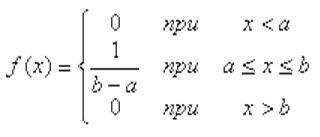

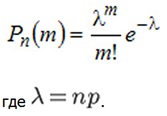
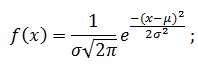
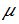 – Математическим ожиданием дискретной случайной величины называют сумму произведений возможных значений случайной величины на вероятности их появления
– Математическим ожиданием дискретной случайной величины называют сумму произведений возможных значений случайной величины на вероятности их появления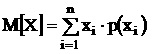
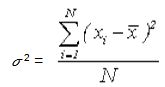
 - среднеквадратическое отклонение случайной величины (квадратный корень из дисперсии.)
- среднеквадратическое отклонение случайной величины (квадратный корень из дисперсии.) График функции нормального распределения, как видно из рисунка, имеет вид куполо¬образной кривой, называемой
График функции нормального распределения, как видно из рисунка, имеет вид куполо¬образной кривой, называемой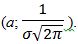 Значит, эта ордината убывает с возрастанием значения
Значит, эта ордината убывает с возрастанием значения 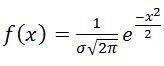

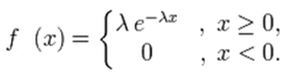
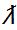 - интенсивность (среднее число событий в единицу времени)
- интенсивность (среднее число событий в единицу времени)

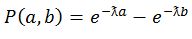
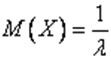 ,математическое ожидание
,математическое ожидание 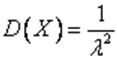 , дисперсия
, дисперсия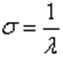 ,среднеквадратическое отклонение
,среднеквадратическое отклонение